Poseidon Hash for ZK Applications

Many use cases of practical computational integrity proof systems such as SNARKs, STARKs, Bulletproofs, involve proving the knowledge of a preimage under a certain cryptographic hash function, which is expressed as a circuit over a large prime field. However, the majority of hash functions do not perform computations in finite field, (SHA-256 in Zcash cryptocurrency). As a result, more constraints must be added in the circuit to represent the operations (for example, XOR, AND, etc.) in hash function as arithmetic operations in finite field. Hence, the expressed circuit could become very expensive due to the enormous number of hash constraints, leading to a huge computational penalty. Therefore, new hash functions that performs natively with ZKP systems are needed.

In 2021, Grassi et al. GKRRS21 introduced $\mathsf{Poseidon}$, a cryptographic hash function that supports arithmetic operations for values in finite field, and therefore friendly with ZK applications. $\mathsf{Poseidon}$ uses $8$ times fewer constraints per message bit than [Pedersen Hash], according to here. The goal of this whole tutorial is to give a simpler explainations about Poseidon hash described in the referenced paper.

Cryptographic sponge functions

$\mathsf{Poseidon}$ is a sponge-based cryptographic hash function, so it is neccessary to understand the design of such hash functions to understand the components of $\mathsf{Poseidon}$. In this section, we look at the definitions and design of a sponged-based cryptographic hash function, before showing its applications in hash functions and other problems.

In 2007, the sponge construction was introduced by Guido Bertoni and others BDPA08.

A sponge construction or sponge function takes input bit data of arbitrary length (called a message) and outputs bit data of fixed length (called a hash digest). In the context of a sponge function, we can say that the message is absorbed to the sponge, and the digest is squeezed out.

A sponge construction hash $2$ phases:

• Absorb: the message is compressed iteratively.
• Squeeze: the digest is extracted iteratively.

Below is the construction of a sponge function:

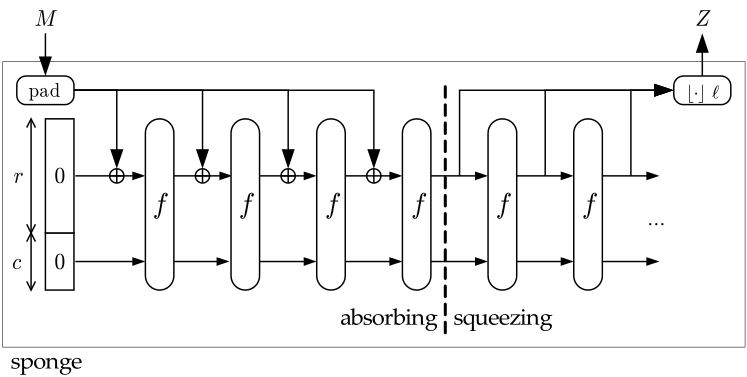
1. The first component (the leftmost) is the state memory $(S)$ and it is divided into $2$ parts: the Bitrate part $(R)$ of size $r$ and the Capacity part $(C)$ of size $c$. $S$ is initially set to $0$, and we denote the initial state as $I$: $I = 0^r || 0^c.$
2. The second component is the compress function $f$ whose input and output are of the same length. $S$ is updated whenever passing the compress function.
3. The third component is the padding function $pad$ which increases the size of the message $M$ to a suitable length (specifically, the length of the padded message is a multiple of bitrate $r$).
4. The squeeze phase takes the Bitrate of $S$ as output parts, before going to the compress function $f$. The final output: $Z = \\{ Z_0; Z_1;...\\}$. If the length of $Z$ is not a multiple of $r$, it will be truncated.

Applications of cryptographic sponge functions

Sponge functions have both theoretical and practical uses. In theoretical cryptanalysis, a random sponge function is a sponge construction where $f$ is a random permutation or transformation, as appropriate. Random sponge functions capture more of the practical limitations of cryptographic primitives than does the widely used random oracle model, in particular the finite internal state BDPA08.

The sponge construction can also be used to build practical cryptographic primitives. For example, $\mathsf{Keccak}$ cryptographic sponge with a $1600$-bit state has been selected by NIST as the winner in the $\mathsf{SHA-3}$ competition. The strength of $\mathsf{Keccak}$ derives from the intricate, multi-round permutation $f$ developed by its authors. The $\mathsf{RC4}$-redesign called $\mathsf{Spritz}$ RS16 refers to the sponge-construct to define the algorithm.

In GKRRS21, they introduced $\mathsf{Poseidon}$ hash function that uses the cryptographic sponge function as its architecture with the compression function $f$ being the permutation $\mathsf{Poseidon}^\pi$.

Poseidon Hash Overview

Now that we understood the architecture of a sponge-based hash function, we are now ready to go to the details of $\mathsf{Poseidon}$. $\mathsf{Poseidon}$ is the proposed hash function in the paper, which maps strings over $\mathbb{F}_p$ (for a prime $p \approx 2^n > 2^{31}$) to fixed length strings over $\mathbb{F}_p$. Specifically, they define: $\mathsf{Poseidon}: \mathbb{F}_p^* \longrightarrow \mathbb{F}_p^o,$ where $o$ is the output length ($\mathbb{F}_p$ elements), usually $o = 1$.

The overall structure of $\mathsf{Poseidon}$ hash is described in the figure below.

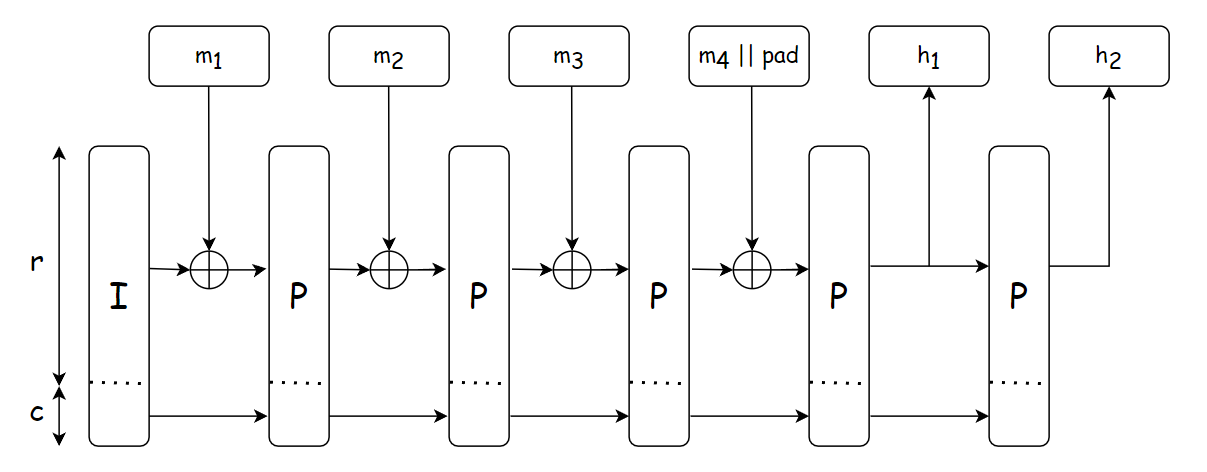
The hash function is constructed by instantiating a sponge function with the compression function $f$ being the permutation $\mathsf{Poseidon}^\pi$ (denoted by the block labeled $\mathsf{P}$ in the figure). The hashing design strategy is based on $\mathsf{Hades}$ GLRRS20, which employes different round functions throughout the permutation to destroy all of its possible symmetries and structural properties.

The workflow of $\mathsf{Poseidon}$ hash is described below, which is used the same in different use cases:

• Determine the capacity value $c$ and the input padding $pad$ depending on each use cases.
• Split the obtained input $m$ in to chunks of size $r$.
• Apply the $\mathsf{Poseidon}^\pi$ permutation to the capacity element and the first chunk: $I_c \oplus m_1$.
• Add the result to the state and apply the permutation again until no more chunks are left.
• Output $o$ output elements from the bitrate part of the state. If needed, iterate the permutation one more time.

Given that the overall structure of $\mathsf{Poseidon}$ is determined by the instatiation of $\mathsf{Poseidon}^\pi$, in the next Sections, we would go to the details of each $\mathsf{Poseidon}^\pi$ block (or equavilently, the block labeled $\mathsf{P}$ in the figure).

Poseidon permutation design

At the heart of the $\mathsf{Poseidon}$ hash is the $\mathsf{Hades}$-based permutation $\mathsf{Poseidon}^\pi$. As mentioned before, $\mathsf{Hades}$ employs efficient round functions which is applied many times in order ti make the permutation behave like a random permutation. The same round function is applied throughout the permutation to destroy its symmetries and structural properties.

This section explains in detail the $\mathsf{Hades}$ design strategy, the detailed design of $\mathsf{Hades}$-based permutation, and the different instantiations of $\mathsf{Poseidon}^\pi$ permutation in different use cases.

Hades design strategy

Overview

In $\mathsf{Hades}$, they mix rounds with full SBox layers and rounds with partial SBox layers. They want to strike the balance between:

• Full layers are expensive in software and ZK proof systems, but well resists statistical attacks.
• Partial layers are computationally cheap, but often serves as good as full ones against algebraic attacks.

Details

The Hades design strategy receives input a state $S=(S_1,S_2,\dots,S_t)$ and consists of $R_f$ initial rounds, in which SBoxes are applied to the full state. After these $R_f$ rounds, $R_p$ partial rounds in the middle contain a single SBox for each round, and the rest of the state goes through the nonliner layer unchanged (you can say that the rest goes through the identity functions $f(x) = x$). Finally, $R_f$ full rounds at the end are applied again: $R_f \longrightarrow R_p \longrightarrow R_f$

An overview of the construction of the permutation can be described in the figure below:

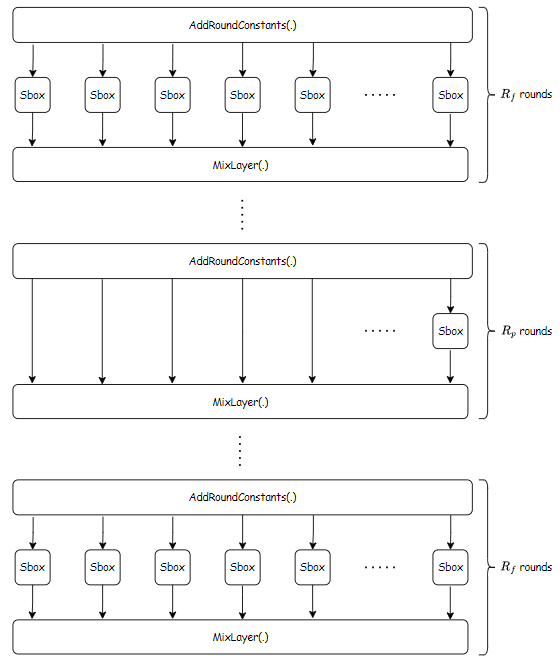
The round function

As in the figure, in each round, several functions (illustrated as the blocks) are applied to the state $S$ to transform it into a new state $S'$, these functions are called round functions. Each round function consists of $3$ components:

• $AddRoundConstants$, denoted by $ARC(\cdot)$: essentially an addition of the state with a random constant.
• $SubWords$, denoted by $SBox(\cdot)$ or $SB(\cdot)$. This is simply the SBox substitution.
• $MixLayers$, denoted by $M(\cdot)$. This is the linear layer of the construction. It involves multiplication between the state and a $t \times t$ MDS(Maximum Distance Separable) matrix. This is used to apply the wide trail strategy (explained in DJRV01) which helps provide arguments against statistical attacks.

Note that: we can use the same number of full rounds instead of partial rounds in the construction without decreasing the security. However, this leads to significantly higher computation costs in our applications.

Maximum Distance Separable

A matrix $M \in \mathbb{F}^{t \times t}$ is called maximum distance saparable (MDS) iff it has a branch number $\mathcal{B}(M) = t + 1$. The branch number of $M$ is defined as $\mathcal{B}(M) = min_{x \in \mathbb{F}^t}\\{wt(x) + wt(M(x))\\}$ where $wt$ is the Hamming weight in wide trail terminology.

Equivalently, a matrix $M$ is MDS iff every submatrix of $M$ is non-singular (a non-singluar matrix is a matrix whose determinant is not $0$). This definition is easier to understand.

There will be a construction of these matrices in later sections, because we do not need regular MDS matrices, but secure MDS matrices.

Hades-based POSEIDON$^\pi$ permutation design

Recall in the previous section, the $\mathsf{Poseidon}^\pi$ permutation is a composition of round functions, each of which consists of $3$ components such as $AddroundConstants$, $SubWords$, and $MixLayer$, each takes input a state $S=(S_1,S_2,\dots,S_t)$ and produces a new state $S'$. In this Section, we describe the $3$ main components of the round function of $\mathsf{Poseidon}^\pi$.

Notation

The function takes input of $t \geq 2$ words in $\mathbb{F}_p$, where $p$ is a prime of size $p \approx 2^n > 2^{30}$ and $N = nt$ to denote the size of texts in bits.

AddRoundConstants component

This is the first component of the round function described in Hades design strategy. Given the input state $S = ( S_1, S_2, \cdots, S_t )$, where each of $S_i$ is a word, it outputs $S' = AddRoundConstants(S, T) = S + T = ( S_1 + T_1, S_2 + T_2, \dots, S_t + T_t )$ where $T$ is the round constant vector that is randomly generated in a method described in Poseidon concrete instantiation. Essentially, this component performs a field addition between the state and the round constant.

The SubWords (SBox) layer

This is the second component of the round function described in Hades design strategy. Subtitution boxes (or S-Boxes) are widely used in cryptography. In this context of an architecture that resembles block ciphers, SBoxes are used to ensure Shannon's property of confusion.

Given the state $S = ( S_1, S_2, \cdots, S_t )$, where each of $S_i$ is a word, this component outputs a new state $S' = SB(S) = ( SB(S_1), SB(S_2), \dots, SB(S_t) ).$ Essentially, this component performs multiple field multiplications on the state.

In GKRRS21, the authors focus on the setting: $SB(x) = x^\alpha, \alpha \geq 3$ where $\alpha$ is the smallest positive integer that satisfies $gcd(\alpha, p - 1) = 1$. These permutations are called "$x^\alpha-Poseidon^\pi$".

Specifically, they use:

• $\alpha = 3$ if $p \not\equiv 1 \pmod{3}$
• $\alpha = 5$ if $p \equiv 1 \pmod{3}$ and $p \not\equiv 1 \pmod{5}$

It turns out that $\alpha = 5$, which is $SB(x) = x^5$, is suitable for the prime subfields of the scalar field of BLS12-381 and BN254, which are two of the most popular prime fields in ZK applications.

MixColumns - The linear layer

This is the last layer (also called the linear layer) of the round function. Given the state $S = ( S_1, S_2, \cdots, S_t )$. This layer outputs the new state

$$S' = \mathcal{M} \times S = \begin{bmatrix}{l} \mathcal{M}\_{11} & \mathcal{M}\_{12} & \dots & \mathcal{M}\_{1t} \\\ \mathcal{M}\_{21} & \mathcal{M}\_{22} & \dots & \mathcal{M}\_{2t} \\\ \dots & \dots & \ddots & \dots \\\ \mathcal{M}\_{t1} & \mathcal{M}\_{t2} & \dots & \mathcal{M}\_{tt} \end{bmatrix} \times \begin{bmatrix} S_1 \\\ S_2 \\\ \dots \\\ S_t \end{bmatrix}$$

where $\mathcal{M}$ is the secure Maximum Distance Separable matrix of size $t \times t$, which is explained in the Hades design strategy. The MDS matrices are randomly and securely generated using a method described in Poseidon concrete instantiations.

It is proved MS78 that a $t \times t$ MDS matrix with elements in $\mathbb{F}_p$ exists if $2t + 1 \leq p$.

One method of constructing such a matrix introduced in this paper is using a Cauchy matrix. For $(x_i, y_i) \in \mathbb{F}\_p$, where $i \in [1, t]$, the entries of the matrix $\mathcal{M}$ are: $\mathcal{M}\_{i, j} = \dfrac{1}{x_i + y_j}$ where the entries of $\\{x_i\\}\_{1 \leq i \leq t}$ and $\\{y_i\\}\_{1 \leq i \leq t}$ are pairwise distinct and $x_i + y_i \neq 0$, where $i \in \\{1,\cdots,t\\}$ and $j \in \\{1,\cdots,t\\}$

Constructing the matrix

The paper suggest the following method to generate matrices to avoid some known vulnerabilities which this note skipped:

• Randomly select pairwise distinct $\\{x_i\\}\_{1 \leq i \leq t}$ and $\\{y_i\\}\_{1 \leq i \leq t}$ where $x_i + y_j \neq 0$ and where $i \in \\{ 1,\cdots,t \\}$ and $j \in \\{ 1,\cdots,t \\}$.
• Determine if the matrix is secure using this test introduced in GRS20
• Repeat this procedure until we find a secure matrix.

Concrete POSEIDON$^\pi$ instantiation

Main instance

• SBox function: The authors proposed using $SB(x)=x^5$ for all use cases
• With the security level $M = 80, 128$, the size of the Capacity $c = 255$ bits ($1$ field element). And $t$ can be $3$ or $5$ to achieve the 2-to-1 or 4-to-1 compression functions.
• Psudeonumber generation: The paper uses Grain LFSR in self-shrinking mode. This can be used to generate the round constants and matrices. This usage can be reminiscent to nothing-up-my-sleeve numbers.
• MDS matrix: It is recommended that we should use the Cauchy matrix for the linear layer, which described in Hades-based permutation design.

The grain LFSR

The grain LFSR is used to generate pseudorandom numbers for the round constants and the MDS matrices described in Hades design strategy. The technical details of the LFSR is provided in Appendix E of GKRRS21. The state in Grain LFSR is $80$ bits in size and is computed as follows:

1. Initialize the state with $80$ bits $\\{b_0,b_1,\cdots,b_{79}\\}$ as follows:
   • $b_0,b_1$: describe the field.
   • $b_2,b_3,b_4,b_5$: describe the SBox.
   • $b_6 \rightarrow b_{17}$: binary representation of $n$.
   • $b_{18} \rightarrow b_{29}$: binary representation of $t$.
   • $b_{30} \rightarrow b_{39}$: binary representation of $R_F$.
   • $b_{40} \rightarrow b_{49}$: binary representation of $R_P$.
   • $b_{50} \rightarrow b_{79}$: set to $1$.
2. Update the bits: $b_{i + 80} = b_{i + 62} \oplus b_{i + 51} \oplus b_{i + 38} \oplus b_{i + 23} \oplus b_{i + 13} \oplus b_i$
3. Discard the first $160$ bits.
4. Evaluate bits in pairs: if the first bit is $1$, output the second bit. If it is $0$, discard the second bit.

If a randomly sampled integer is $\geq p$, we discard this value and take the next one. We generate numbers starting from the most significant bit. However, starting from MSB or LSB makes no difference regarding the security

Choosing number of rounds

Proved in Proposition 5.1, 5.2, and 5.3 in GKRRS21, this table represents the parameters $R_F, R$ that can protect the construction from statistical and algebraic attacks:

Construction	$R_F$	$R = R_F + R_P$
$x^5$-$\mathsf{Poseidon}$-$128$	$6$	$56 + \lceil \log_5{(t)} \rceil$
$x^5$-$\mathsf{Poseidon}$-$80$	$6$	$35 + \lceil \log_5{(t)} \rceil$
$x^5$-$\mathsf{Poseidon}$-$256$	$6$	$111 + \lceil \log_5{(t)} \rceil$