Cryptographic sponge functions

\(\mathsf{Poseidon}\) is a sponge-based cryptographic hash function, so it is neccessary to understand the design of such hash functions to understand the components of \(\mathsf{Poseidon}\). In this section, we look at the definitions and design of a sponged-based cryptographic hash function, before showing its applications in hash functions and other problems.

In 2007, the sponge construction was introduced by Guido Bertoni and others [BDPA08].

A sponge construction or sponge function takes input bit data of arbitrary length (called a message) and outputs bit data of fixed length (called a hash digest). In the context of a sponge function, we can say that the message is absorbed to the sponge, and the digest is squeezed out.

A sponge construction hash \(2\) phases:

• Absorb: the message is compressed iteratively.
• Squeeze: the digest is extracted iteratively.

Below is the construction of a sponge function:

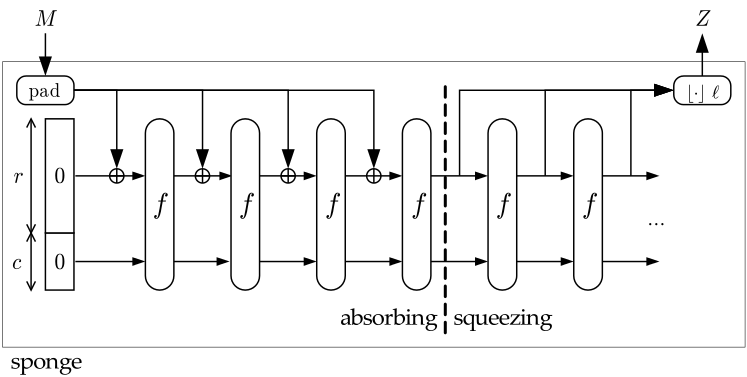
1. The first component (the leftmost) is the state memory \((S)\) and it is divided into \(2\) parts: the Bitrate part \((R)\) of size \(r\) and the Capacity part \((C)\) of size \(c\). \(S\) is initially set to \(0\), and we denote the initial state as \(I\): $$I = 0^r || 0^c.$$
2. The second component is the compress function \(f\) whose input and output are of the same length. \(S\) is updated whenever passing the compress function.
3. The third component is the padding function \(pad\) which increases the size of the message \(M\) to a suitable length (specifically, the length of the padded message is a multiple of bitrate \(r\)).
4. The squeeze phase takes the Bitrate of \(S\) as output parts, before going to the compress function \(f\). The final output: \(Z = \{ Z_0; Z_1;...\} \). If the length of \(Z\) is not a multiple of \(r\), it will be truncated.

Applications of cryptographic sponge functions

Sponge functions have both theoretical and practical uses. In theoretical cryptanalysis, a random sponge function is a sponge construction where \(f\) is a random permutation or transformation, as appropriate. Random sponge functions capture more of the practical limitations of cryptographic primitives than does the widely used random oracle model, in particular the finite internal state [BDPA08].

The sponge construction can also be used to build practical cryptographic primitives. For example, \(\mathsf{Keccak}\) cryptographic sponge with a \(1600\)-bit state has been selected by NIST as the winner in the \(\mathsf{SHA-3}\) competition. The strength of \(\mathsf{Keccak}\) derives from the intricate, multi-round permutation \(f\) developed by its authors. The \(\mathsf{RC4}\)-redesign called \(\mathsf{Spritz}\) [RS16] refers to the sponge-construct to define the algorithm.

In [GKRRS21], they introduced \(\mathsf{Poseidon}\) hash function that uses the cryptographic sponge function as its architecture with the compression function \(f\) being the permutation \(\mathsf{Poseidon}^\pi\).