Poseidon Hash Overview

Now that we understood the architecture of a sponge-based hash function, we are now ready to go to the details of \(\mathsf{Poseidon}\). \(\mathsf{Poseidon}\) is the proposed hash function in the paper, which maps strings over \(\mathbb{F}_p\) (for a prime \(p \approx 2^n > 2^{31}\)) to fixed length strings over \(\mathbb{F}_p\). Specifically, they define: $$\mathsf{Poseidon}: \mathbb{F}_p^* \longrightarrow \mathbb{F}_p^o,$$ where \(o\) is the output length (\(\mathbb{F}_p\) elements), usually \(o = 1\).

The overall structure of \(\mathsf{Poseidon}\) hash is described in the figure below.

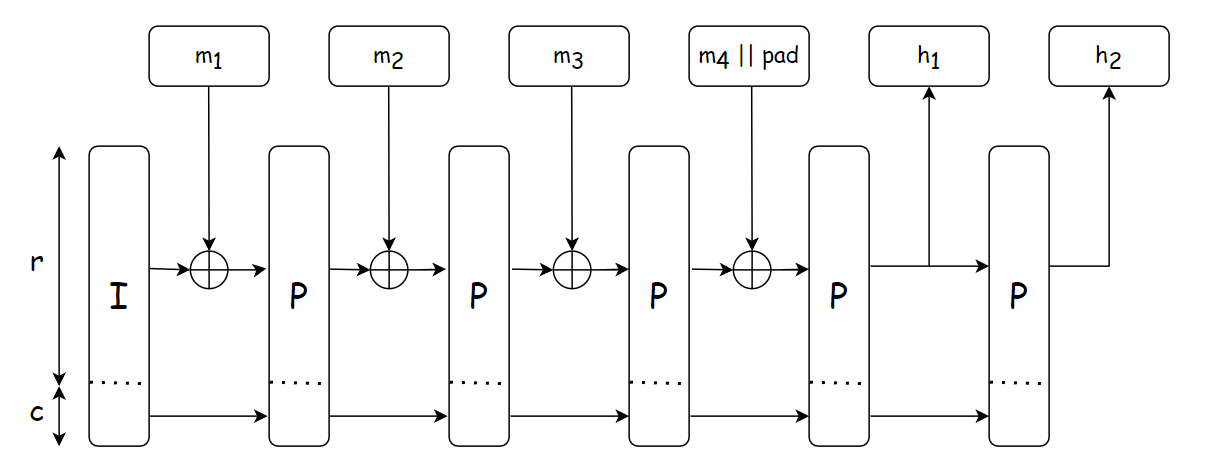
The hash function is constructed by instantiating a sponge function with the compression function \(f\) being the permutation \(\mathsf{Poseidon}^\pi\) (denoted by the block labeled \(\mathsf{P}\) in the figure). The hashing design strategy is based on \(\mathsf{Hades}\) [GLRRS20], which employes different round functions throughout the permutation to destroy all of its possible symmetries and structural properties.

The workflow of \(\mathsf{Poseidon}\) hash is described below, which is used the same in different use cases:

• Determine the capacity value \(c\) and the input padding \(pad\) depending on each use cases.
• Split the obtained input \(m\) in to chunks of size \(r\).
• Apply the \(\mathsf{Poseidon}^\pi\) permutation to the capacity element and the first chunk: \(I_c \oplus m_1\).
• Add the result to the state and apply the permutation again until no more chunks are left.
• Output \(o\) output elements from the bitrate part of the state. If needed, iterate the permutation one more time.

Given that the overall structure of \(\mathsf{Poseidon}\) is determined by the instatiation of \(\mathsf{Poseidon}^\pi\), in the next Sections, we would go to the details of each \(\mathsf{Poseidon}^\pi\) block (or equavilently, the block labeled \(\mathsf{P}\) in the figure).