Hades design strategy
Overview
In \(\mathsf{Hades}\), they mix rounds with full SBox layers and rounds with partial SBox layers. They want to strike the balance between:
- Full layers are expensive in software and ZK proof systems, but well resists statistical attacks.
- Partial layers are computationally cheap, but often serves as good as full ones against algebraic attacks.
Details
The Hades design strategy receives input a state \(S=(S_1,S_2,\dots,S_t)\) and consists of \(R_f\) initial rounds, in which SBoxes are applied to the full state. After these \(R_f\) rounds, \(R_p\) partial rounds in the middle contain a single SBox for each round, and the rest of the state goes through the nonliner layer unchanged (you can say that the rest goes through the identity functions \(f(x) = x\)). Finally, \(R_f\) full rounds at the end are applied again: $$R_f \longrightarrow R_p \longrightarrow R_f$$
An overview of the construction of the permutation can be described in the figure below:
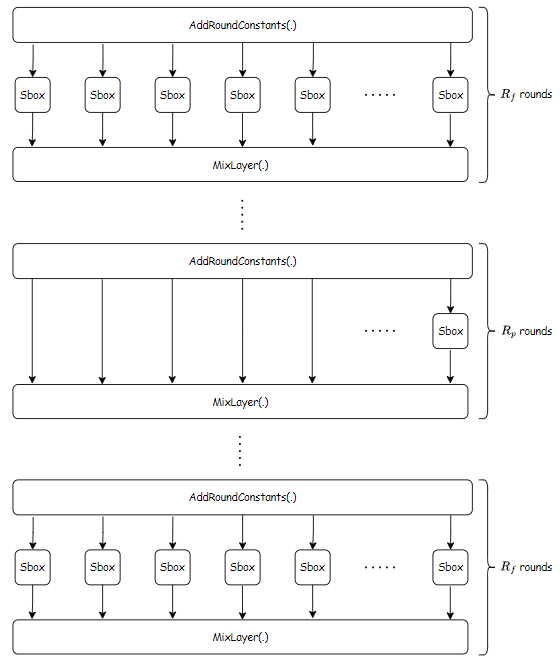
The round function
As in the figure, in each round, several functions (illustrated as the blocks) are applied to the state \(S\) to transform it into a new state \(S'\), these functions are called round functions. Each round function consists of \(3\) components:
- \(AddRoundConstants\), denoted by \(ARC(\cdot)\): essentially an addition of the state with a random constant.
- \(SubWords\), denoted by \(SBox(\cdot)\) or \(SB(\cdot)\). This is simply the SBox substitution.
- \(MixLayers\), denoted by \(M(\cdot)\). This is the linear layer of the construction. It involves multiplication between the state and a \(t \times t\) MDS(Maximum Distance Separable) matrix. This is used to apply the wide trail strategy (explained in [DJRV01]) which helps provide arguments against statistical attacks.
Note that: we can use the same number of full rounds instead of partial rounds in the construction without decreasing the security. However, this leads to significantly higher computation costs in our applications.
Maximum Distance Separable
A matrix \(M \in \mathbb{F}^{t \times t}\) is called maximum distance saparable (MDS) iff it has a branch number \(\mathcal{B}(M) = t + 1\). The branch number of \(M\) is defined as \(\mathcal{B}(M) = min_{x \in \mathbb{F}^t}\{wt(x) + wt(M(x))\}\) where \(wt\) is the Hamming weight in wide trail terminology.
Equivalently, a matrix \(M\) is MDS iff every submatrix of \(M\) is non-singular (a non-singluar matrix is a matrix whose determinant is not \(0\)). This definition is easier to understand.
There will be a construction of these matrices in later sections, because we do not need regular MDS matrices, but secure MDS matrices.